近年IT化が進むにつれてビッグデータと呼ばれる、人間では読み切ることができないような膨大な情報が手に入るようになりました。これらの情報は統計学を用いて解読し、意味を持たせることができます。今回は解読方法の一つであるZ検定について解説いたします。Z検定は大学数学の統計で扱う初歩的な検定方式なので、統計学に触れたことが無い方も理解できると思います!
ある塾会社がある資格に対して、塾の教育を受ければ平均的に60点をとれることを宣伝しています。受講生は大量におり、母分散は既知で16点であると発表しています。40人に対し調査を行い、40人の平均が53点であるということが判明しました。
この場合、塾会社が発表している平均60点という数値は偽りであるといえるでしょうか。
じつは母分散が既知で、サンプル数が十分大きいこの特殊な状況に限り、z検定が使えます。
この場合、塾会社が発表している平均60点という数値は偽りであるといえるでしょうか。
じつは母分散が既知で、サンプル数が十分大きいこの特殊な状況に限り、z検定が使えます。
\bar{X}=標本平均(サンプルの平均) \\\\{ μ_0 }=母平均(塾が主張する平均)\\\\{σ}=母標準偏差\\\\{n}=サンプル数(調査を行った人数)とあてはめます。これらを
\frac{\bar{X}ー { μ_0 }
}{\frac{σ}{\sqrt{n}}}という式にそれぞれあてはめると、
\frac{{53}ー { 60 }
}{\frac{4}{\sqrt{40}}}=-11.067961811058...となります。この数値の絶対値と、95%信頼区間のx軸の値である1.96を比較すると、11.06796…の方がはるかに上回っていますね。上回っている場合、棄却され、塾会社が発表している平均60点という数値は偽りであるといえます。
なぜこうであるといえるのでしょうか。一つ一つ説明していきます!
まず世の中の色々な事象は正規分布(ガウス分布)に従うということがしられています。(下図)
上の例を用いますと、塾に通う資格受験者が無限であるとしましょう。この無限の塾に通う資格受験者の各点数をまとめたものを、母集団と呼びます。この母集団からランダムにn個のサンプル(点数)を抽出します。そしてそのサンプルの平均を求めます。この平均をaとしましょう。この作業を何回も繰り返します。そうすると平均が56, 62, 50… など繰り返した分でてきます。それらの値を横軸にプロットします。縦軸には相対度数(各点数の平均の数の割合)をプロットします。
そうすると横軸に50, 56, 62…とならび、縦軸にはサンプルの平均が50だったサンプルの割合が横軸50の縦軸にプロットされ、56の縦軸には平均が56のサンプルがどれぐらいあるかという割合がプロットされ、それを大量に行います。
この作業を行う時に、n(一回のサンプリングの時にとるデータの数)が大きければ大きいほど正規分布に近似してくるのです。これは中心極限定理として知られています。
まず世の中の色々な事象は正規分布(ガウス分布)に従うということがしられています。(下図)
上の例を用いますと、塾に通う資格受験者が無限であるとしましょう。この無限の塾に通う資格受験者の各点数をまとめたものを、母集団と呼びます。この母集団からランダムにn個のサンプル(点数)を抽出します。そしてそのサンプルの平均を求めます。この平均をaとしましょう。この作業を何回も繰り返します。そうすると平均が56, 62, 50… など繰り返した分でてきます。それらの値を横軸にプロットします。縦軸には相対度数(各点数の平均の数の割合)をプロットします。
そうすると横軸に50, 56, 62…とならび、縦軸にはサンプルの平均が50だったサンプルの割合が横軸50の縦軸にプロットされ、56の縦軸には平均が56のサンプルがどれぐらいあるかという割合がプロットされ、それを大量に行います。
この作業を行う時に、n(一回のサンプリングの時にとるデータの数)が大きければ大きいほど正規分布に近似してくるのです。これは中心極限定理として知られています。
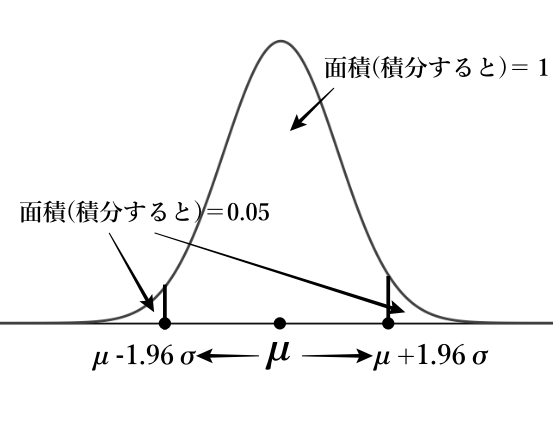
正規分布にグラフが変化すると、サンプリングした各平均の平均、つまりμは同時に中央値になります。さらにμから1.96倍した標準偏差分横軸を離れると、中央部分に95%のデータが集まっていることが知られています。つまり平均から1.96σ以上離れたデータは5%しかないということです。この事実を使い検証ができるわけです。
例に戻りましょう。我々は一回サンプリングをし、平均が53点であるという結果を得ました。中心極限定理の条件であるnが十分大きいということに関しては、一般的に30以上が妥当とされていますので、40人に調査を行った我々はクリアしています。よってこの53点は正規分布に従っているグラフのどこかにあるだろうということがわかるのです。
正規分布を扱いやすくするために、標準化というものを行い、分散を1、平均を0にします。こうすると、標準正規分布にあてはめることができ、平均である0から1.96離れているかどうかで検討できるようになります。
よって
\frac{{53}ー { 60 }
}{\frac{4}{\sqrt{40}}}=-11.067961811058...という式が導出され、この絶対値が1.96を大いに上回っているため、棄却させることになります。
